洛谷P3956 [NOIP2017 普及组] 棋盘
前言
本蒟蒻怎么就这么喜欢发noip csp的题呢(
一个绿题,风光啊 QwQ
题面
点只因查看题面
题目背景
NOIP2017 普及组 T3
题目描述
有一个的棋盘,棋盘上每一个格子可能是红色、黄色或没有任何颜色的。你现在要从棋盘的最左上角走到棋盘的最右下角。
任何一个时刻,你所站在的位置必须是有颜色的(不能是无色的), 你只能向上、 下、左、 右四个方向前进。当你从一个格子走向另一个格子时,如果两个格子的颜色相同,那你不需要花费金币;如果不同,则你需要花费 $1 $个金币。
另外, 你可以花费 个金币施展魔法让下一个无色格子暂时变为你指定的颜色。但这个魔法不能连续使用, 而且这个魔法的持续时间很短,也就是说,如果你使用了这个魔法,走到了这个暂时有颜色的格子上,你就不能继续使用魔法; 只有当你离开这个位置,走到一个本来就有颜色的格子上的时候,你才能继续使用这个魔法,而当你离开了这个位置(施展魔法使得变为有颜色的格子)时,这个格子恢复为无色。
现在你要从棋盘的最左上角,走到棋盘的最右下角,求花费的最少金币是多少?
输入格式
第一行包含两个正整数$ m, n$,以一个空格分开,分别代表棋盘的大小,棋盘上有颜色的格子的数量。
接下来的$ n x, y, c(x,y) c$。
其中$ c=1$ 代表黄色,$ c=0$ 代表红色。 相邻两个数之间用一个空格隔开。 棋盘左上角的坐标为,右下角的坐标为。
棋盘上其余的格子都是无色。保证棋盘的左上角,也就是 一定是有颜色的。
输出格式
一个整数,表示花费的金币的最小值,如果无法到达,输出。
样例 #1
样例输入 #1
1 | 5 7 |
样例输出 #1
1 | 8 |
样例 #2
样例输入 #2
1 | 5 5 |
样例输出 #2
1 | -1 |
提示
输入输出样例 1 说明
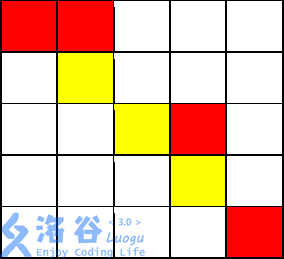
从开始,走到不花费金币
从向下走到花费 枚金币
从施展魔法,将变为黄色,花费 枚金币
从走到不花费金币
从走到不花费金币
从走到花费 枚金币
从走到花费 枚金币
从施展魔法,将变为黄色,花费$ 2$ 枚金币,
从走到不花费金币
从走到花费 枚金币
共花费 $8 $枚金币。
输入输出样例 2 说明
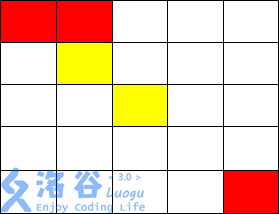
从走到,不花费金币
从走到,花费$ 1 $金币
施展魔法将变为黄色,并从走到花费$ 2$ 金币
从走到不花费金币
从只能施展魔法到达
而从以上四点均无法到达,故无法到达终点,输出
数据规模与约定
对于 的数据, 。
对于 的数据, 。
对于 的数据, 。
思路
怎么走
本蒟蒻不会某些大佬的 MBFS Dijkstra 图论 SPFA 什么的,遂采用记忆化DFS+剪枝。 其实这是QYC布置的离dfs神犇一步之遥题单
我们定义一个函数 dfs(x,y,coin,can,color)
x,y表示坐标,coin表示当前的金币数量,color表示当前坐标的颜色,can表示当前是否能施展魔法。
再加一个mp数组记录颜色,-1表示无颜色,0表示红色,1表示黄色
为什么不直接使用 mp[x][y] 获取颜色呢?从题目中可知,如果下一个格子没有颜色,需要施展“魔法”改变颜色才可以移动,而且这个魔法是临时的,离开之后就会复原,所以需要传一个颜色进去,不然会影响下一步的颜色判定。
与大部分棋盘类dfs相似,我们定义两个数组fx,fy来记录每个方向两轴的变化:const int fx[5]={0,-1,1,0,0},fy[5]={0,0,-1,1},写一个1-4的循环,每一次的nx,ny(下一个方向的坐标)就为x+fx[i],y+fy[i]。
搜索就很简单了,如果mp[nx][ny]==color,那么直接搜索:
dfs(nx,ny,coin,1,color);
不然的话,如果mp[nx][ny]!=-1(即不是无颜色),搜索,并将金币+1:
dfs(nx,ny,coin+1,1,mp[nx][ny]);
否则就没有颜色了,施展魔法将其变为当前格子颜色,因为魔法只能施展一次,前面的can变量就起效了,如果上一次施展过魔法,can为0,就不可以走这个格子了,然后金币+2,即mp[nx][ny]==-1&&can&&coin+2<minmp[nx][ny]。
dfs(nx,ny,coin+2,0,color);
接下来我们需要一些边界条件,如果到达目标点,即为x==m&&y==m时,退出循环并记录最小值。如果x和y超过合法范围也要返回:
1 | if(x>m||y>m||x<1||y<1) return; |
除此之外,你需要一个vis数组记录当前走过的部分(回溯!!!),不然你会得到壮观的MLE:

这就是简单的搜索逻辑。
剪枝
作为一个普及组的第三题,哪有那么容易让你拿分呢?
终于,你写出了代码,你披星戴月、奋不顾身,只为证明——只因它太暴力:

1 |
|
显然,她需要剪枝。
对于剪枝来说,有这几种思路:
- 发现当前金币已经比最小的多了,就不用搜下去了
- 在循环中就可以判断搜索合法性了,减小函数调用开销(PS:我习惯把这玩意写在边界条件上面,看起来差不多,实则增加了函数调用开销,调用后才返回,花费显然很大
- 记忆化,记录走到当前坐标合法路径的最小金币,如果超过就可以不搜了,比第一个更高级
关于记忆化,我们可以定义一个数组minmp[1145][1145]并初始化为inf(用memset需要改为127)
然后在循环里面判断即可。
代码
终于可以上代码了:
我已经认真读完并理解了上面的解析,并且不会直接照搬
1 |
|